Abstract: Based on the analysis and comparison of existing grid resource management models, a concrete model based on layered structure HRMM is proposed, which divides resource management into job parallel analysis, global resource allocation, local resource allocation and There are four levels of local resource management, and corresponding optimization strategies and algorithms are designed for each level. The maximum computational complexity of this model for resource management is O (n2) ~ O (n3), which is an optimized and effective grid resource management model. Computing grid is an important parallel distributed computing technology that has emerged in recent years. One of its key technologies is to manage the resources in the grid. The resources in the grid have wide-area distribution, heterogeneous and dynamic characteristics, which makes grid resource management very complicated. There is currently no model that can handle all grid application needs. At present, grid resource management models are mainly divided into three categories: layered model, abstract owner model and economic / market model. The Globus project team has an important voice in formulating the grid protocol. Many important companies including IBM, Microsoft, Sun, Compaq, SGI, and NEC have announced support for the Globus Toolkit. Therefore, the layered model adopted by Globus represents the development trend of grid resource management. This paper proposes an optimized grid resource management model HRMM (Hierarchical Resource Management Model) on the basis of Globus layered model design ideas, and gives the corresponding resource management algorithm. In order to improve efficiency, the data structure and interface provided by Globus Toolkit 2.4 are used in the main modules of HRMM. The design idea of ​​HRMM is to dynamically receive job requests from users and allocate qualified computing resources for the jobs, while providing online feedback on resource information during the entire computing process and accepting users' online control. The architecture of HRMM is shown in Figure 1. The resource management tasks of the computing grid are divided into four levels: job parallel analysis, global resource allocation, local resource allocation, and local resource management. As can be seen from Figure 1, the user submits a job request to HRMM through the GUI (Graphical User Interface), the job parallel analyzer receives the user's job request, and then divides the tasks in the job into several task groups according to the maximum parallelism, and submits them to the global resource allocation Device. For each task in the multi-task group, the global resource allocator searches multiple clusters that meet the demand in the static resource library at one time, and forms a candidate cluster group to submit to the local resource allocator. The local resource allocator reads the relevant information of each cluster in the candidate cluster group in the dynamic resource library, and allocates the corresponding task to the cluster that meets the most conditions. Then, the cluster applies the local resource manager to perform the task. On the whole, the local resource manager sends static resource update information to the static resource library at regular intervals. In addition, before the local resource allocator reads the dynamic resource library, the dynamic resource library will read the update information from the local resource manager. In this hierarchical model, on the one hand, the jobs submitted by users can be executed with the greatest degree of parallelism, which effectively reflects the idea of ​​parallel computing; on the other hand, multiple clusters are selected to form a candidate cluster group, and then one of them is determined. The resource allocation scheme takes into account the static and dynamic requirements of the task and avoids repeated query operations, thereby improving the efficiency of resource allocation. 2 Job Parallel Analyzer As shown in Figure 1, the user submits a job request to the job parallel analyzer via the GUI. This request includes information about multiple tasks contained in the job, the dependencies between tasks, and the computing resource requirements of each task. The job parallel analyzer analyzes the tasks and their interrelationships in the job, divides the tasks in the job into different task groups according to the dependencies of each task, and describes each task group appropriately before submitting it to the global resource allocator. 2.1 Topological representation of the job A job consists of one or more tasks. The topology of the job is defined as a directed acyclic graph that satisfies the following conditions: the nodes in the graph correspond to the tasks in the job one by one; if task B directly depends on task A, there is a directed from node A to node B Edge, A is called the direct precursor of B, and B is the direct successor of A; if there is a directed path from A to B composed of multiple directed edges, then A is called the precursor of B, and B is the successor of A . Figure 2 shows the topology of a job. Assume that the job consists of 7 tasks marked A ~ G and their interrelationships. As shown in Figure 2, task D needs to start after tasks A and B are completed, while task G must start after tasks are completed with F. In order to improve the efficiency of parallel execution of jobs, it is necessary to pay attention to the depth of tasks in the topology definition. Remember that the direct precursor set of task T is Pd (T), then its depth d (T) is: If Pd (T) = φ, then d (T) = 1; If Pd (T) ≠φ, then d (T) = max {d (R)} + 1. R∈Pd (T) 2.2 Division of the maximum parallelism of the job The parallel division of jobs refers to: a series of task groups formed after a job is split corresponding to each task, in order and independent of each other. A job can have one or more parallel partition schemes, forming a parallel partition set corresponding to the job, denoted as Θ, and I (Θ) is the number of task groups in Θ. This is called the maximum parallelism division of the job, if: E ∈ Θ, and ξ ∈ Θ. I () ≤I (ξ) divides multiple tasks in the job according to the corresponding depth to form a maximum parallel degree division For the job in Figure 2, its maximum parallelism is divided into: = {(A, B), (C, D, E), F, G}. After receiving the task group described in RSL, the global resource allocator immediately analyzes and interprets it to obtain the static resource requirements of each task. The system searches for multiple clusters in the static resource library according to the resource requirements of each task, and submits the results to the local resource allocator. 3.1 Static resource library The static resource library in the system adopts LDAP structure based on lightweight directory access protocol. In the HRMM model, all the static resources of the grid system have established corresponding directory items in the DIT (directory information tree) of the LDAP server, and use the combination of <attribute, value> to describe various resource attributes. Static LDAP selection of LDAP can bring the following advantages in performance: (1) LDAP specifically optimizes the read operation. In the case of frequent read operations, the read efficiency can be improved. (2) LDAP is a cross-platform protocol that can be used on any computer. Thereby increasing the adaptability of the system to the heterogeneous grid environment. (3) The LDAP server supports a distributed structure, and the static resource library can access the local or global LDAP server, and can easily achieve synchronization, that is, enhance the distribution of resource management. 3.2 Global resource allocation algorithm According to the static demand of each task in the task group, the global resource allocator searches for the cluster that meets the demand in the static resource library. During the search, the starting position of the search is randomly selected, and then for each task, the first N clusters that meet the needs of the task are returned to form a candidate cluster group, which is described by the ClusterList data structure and submitted to local resource allocation. Among them, ClusterList is used to describe the generalized table structure of the candidate cluster group, as shown in Figure 3. For any task, if only K ( 4 Local resource allocator The local resource allocator searches the dynamic resource library for the dynamic information of the candidate cluster group, combines these dynamic information with the static information obtained from the global resource allocator, and performs a comprehensive analysis, and finally assigns each task in the task group to The most suitable cluster. 4.1 Dynamic Resource Library The data in the dynamic resource library is described in XML, which brings the following advantages: (1) XML is optimized for update operations. Therefore, for a dynamic resource library that needs to be constantly updated, efficiency can be effectively improved. (2) Both XML and LDAP have a tree structure in storage structure, which can be easily converted into each other. Using XML to describe data can make the dynamic resource library and LDAP-based static resource library have better coupling. (3) XML has nothing to do with the platform, and the data expressed in XML can be easily used by other programs. 4.2 Local resource allocation strategy After the local resource allocator obtains the cluster list of candidate cluster groups, it obtains the dynamic information of each candidate cluster from the dynamic resource library, adds these dynamic information to the static information of the corresponding cluster, and then combines the static resources and dynamic resource information. Form cluster comprehensive resource information. Let the dynamic resource information of a cluster be h = [h1, ..., hm] T, and the static resource information t = [t1, ..., td] T, where m and d are the number of fields described by the dynamic and static resources, respectively, then The cluster comprehensive information is υ = [tThT] T = [υ1, ..., υp] T, where P = m + d. As shown in Fig. 3, the comprehensive information of clusters 2 and 2 is represented as v2.2. Similarly, combining the static resource requirements and dynamic resources of a task, let the dynamic resource requirements of a task be g = [g1, ..., gm] T, and the static resource requirements are s = [s1, ..., sd) T, then comprehensive resources The demand is r = [sT gT] T = [r1, ..., rp] T. The comprehensive resource requirement for task i is expressed as ri. When determining the allocation strategy, only the comprehensive resource requirements of the task and the comprehensive resource information of the cluster will be considered. First, in order for the task to be completed successfully, the selected cluster must meet both the static resource requirements and the dynamic resource requirements of the task, that is, the comprehensive resource requirements of the task: ∨i∈ [1, n], ∨j∈ [1, p], Vi, f (i) [j] ≥ri [j] Where n is the number of tasks in the task group, p is the dimension of the vector u / and r, and f (i) is the sequence number of the selected cluster in the candidate cluster of task i (that is, the cluster list corresponding to Taski in ClusterList). Therefore, first delete all clusters that do not meet the above conditions in ClusterList, and note that there are Ki candidate clusters that meet the comprehensive resource requirements for the i-th task, where 1≤i≤n and 1≤Ki≤N. Finally, the local resource allocator chooses the most suitable one from Ki candidate clusters for each task Taski. Comprehensively considering the overall resource allocation efficiency of the computing grid, the following decision-making mechanism is adopted when specifically selecting the cluster: (1) The comprehensive resource information of the selected cluster should be as close as possible to the comprehensive resource requirements of the corresponding tasks to avoid waste of resources, namely: (2) The total network delay between the selected cluster and the task submission node should be as small as possible, namely: Where tj is the delay of the cluster with the global identifier j; (3) HRMM stipulates the upper limit of computing resource consumption for each user, namely: Where W is the upper limit of the user's occupation of computing resources, and W> 0. Considering the above three aspects comprehensively, local resource allocation can be described as the following secondary planning problem: Where C is a weighting factor that can be changed, and C> 0. Since f (i) is a discrete value and the range of values ​​is limited, the following optimization method is proposed to search for the approximate optimal solution with less calculation. If the candidate cluster group is ClusterList, the algorithm is expressed as follows: STEP 1. For each task and candidate cluster, combine static and dynamic resource information into comprehensive resource information; STEP 2. Delete clusters in ClusterList that do not meet the total resource requirements; STEP 3. STEP 4. Sort each column of Cost in parallel and rearrange the cluster list in ClusterList in ascending order; STEP 5. in case STEP 6. ∨i∈ [1, n], parallel calculation Cost * [i]: = ‖vi, k-ri‖ + C · TI, k, where k = aramin (‖vi, j‖ <‖vi, 1‖); STEP 7. ∨i∈ [1, n], parallel calculation d (i): = STEP 8. Set b: = argmin (d [j]), and delete the first k-1 cluster nodes in the cluster list of task b in ClusterList; STEP 9. If satisfied STEP 10. ∨i∈ [1, n], assign the ith task to the first cluster in the cluster list of the corresponding task cluster in ClusterList, and the algorithm ends. The algorithm finds an approximate optimal solution for resource allocation, and maximizes the use of the computing resources of the cluster where the resource management site is located to parallelize most of the calculations. If the number of nodes in the cluster where the resource management site is located is a household, the computational complexity of the algorithm on each node is O (n2n / P) 5 Analysis and summary This research group adopts a structure based on a hierarchical model, divides resource management into four levels, and then optimizes the performance of the model at each level and proposes corresponding algorithms. Overall, the maximum computational complexity of HRMM for resource management of a job does not exceed O (n3), which is an optimized and effective grid system resource management model. Smart Board For Conference,Whiteboard Smart Board,Interactive Whiteboard Smart Board,Smart Board Interactive Whiteboard ALLIN , https://www.displayapio.com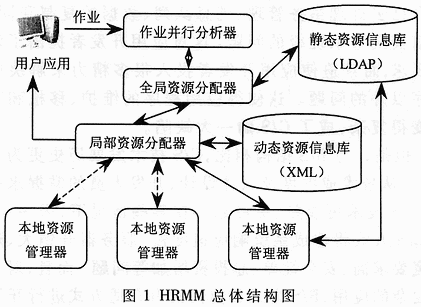
1 The overall structure of HRMM 
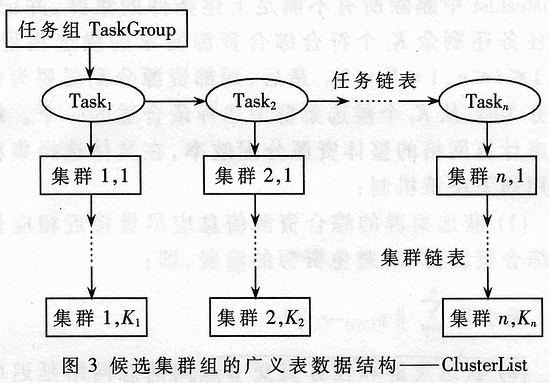
3 Global resource allocator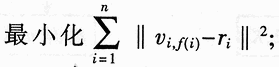 
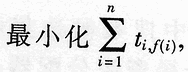
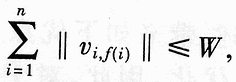
, Calculate the local loss Cost [i, j] of each cluster i, j: = ‖vi, j-ri‖ + C · TIj;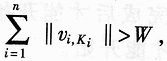 
, Then report that there is no solution that satisfies the condition, and the algorithm ends;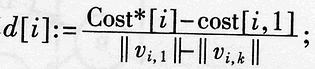 
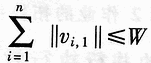Turn to STEP10, otherwise turn to STEP6;
May 28, 2025