Introduction to statistical indicators for classification problems: confusion matrix, recall, false positive rate, AUROC
Abbreviation
Area Under the Curve (AUC)
Area Under the Receiver Operating Characteristic Curve (AUROC)
In most cases, AUC is used to refer to AUROC, which is not a good practice. As Marc Claesen has pointed out, AUC can be ambiguous since it could refer to any curve, while AUROC is more specific and clear.
What is AUROC?
AUROC can be interpreted in several equivalent ways:
The probability that a randomly selected positive instance is ranked higher than a randomly selected negative one.
The expected proportion of positive samples that are ranked before random negative samples.
The expected true positive rate when the ranking is such that a random negative sample comes after a random positive one.
The expected false positive rate when the ranking is such that a random positive sample comes before a random negative one.
For a deeper understanding, you can check this detailed explanation on Stack Exchange: How to derive the probabilistic interpretation of AUROC.
How is AUROC calculated?
Suppose we have a binary classifier that outputs probabilities, like logistic regression. Before discussing the ROC curve, it's important to understand the concept of the confusion matrix. A binary classification model can result in four possible outcomes:
- Predicted 0, Actual 0: This is called True Negative, meaning the model correctly predicted a negative outcome. For example, an antivirus program doesn't flag a harmless file as a virus.
- Predicted 0, Actual 1: This is a False Negative, meaning the model incorrectly predicted a negative outcome when it was actually positive. For example, an antivirus fails to detect a real virus.
- Predicted 1, Actual 0: This is a False Positive, meaning the model incorrectly predicted a positive outcome when it was actually negative. For example, an antivirus flags a harmless file as a virus.
- Predicted 1, Actual 1: This is a True Positive, meaning the model correctly predicted a positive outcome. For example, an antivirus identifies a real virus.
Based on these four outcomes, we can build a confusion matrix, which summarizes the performance of the model.

In the example above, out of 50 data points, 45 were correctly classified, and 5 were misclassified.
When comparing different models, it's often useful to use a single performance metric instead of multiple ones. To do this, we calculate two key metrics from the confusion matrix:
True Positive Rate (TPR), also known as sensitivity, recall, or hit rate, is defined as TP / (TP + FN). It measures the proportion of actual positives that are correctly identified. A higher TPR means fewer positive instances are missed.
False Positive Rate (FPR), also known as the fall-out, is defined as FP / (FP + TN). It measures the proportion of actual negatives that are incorrectly identified as positives. A higher FPR means more negative instances are misclassified.
By varying the decision threshold (e.g., 0.00, 0.01, ..., 1.00), we can compute TPR and FPR at each threshold and plot them on a graph where the x-axis is FPR and the y-axis is TPR. This curve is called the ROC curve, and the area under this curve is the AUROC.
The image below shows an example of an AUROC curve:
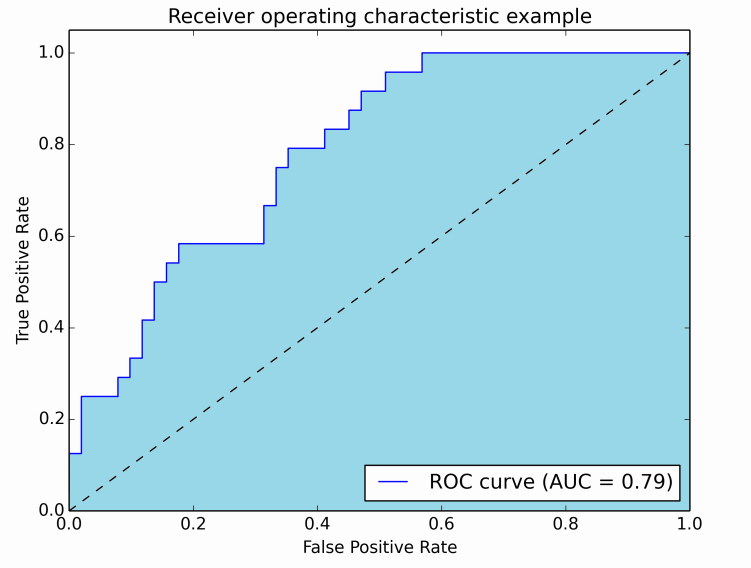
In the figure, the blue area represents the AUROC. The dashed diagonal line corresponds to a random classifier, which has an AUROC of 0.5. This line serves as a baseline to determine whether a model performs better than random guessing.
If you want to try it yourself:
Python: Scikit-learn ROC Example
MATLAB: MathWorks Documentation
For One Plus Edge Glass,Oneplus 10 Pro Glass,Oneplus 10 Pro Glass Screen,Oneplus 8 Pro Screen Glass
Dongguan Jili Electronic Technology Co., Ltd. , https://www.jlglassoca.com